Adaptive Chosen-Plaintext Deep Learning-Based Side-Channel Analysis

文章信息

• 作者：Yanbin Li^1,2,3，Yuxin Huang⁴，Yikang Guo⁴，Chunpeng Ge¹，Fanyu Kong¹，Yongjun Ren⁵。

• 单位：

  1. School of Software, Shandong University, Jinan, China, 250101
  2. State Key Laboratory of Cryptology, P.O.Box 5159, Beijing, China, 100878
  3. Henan Key Laboratory of Network Cryptography Technology
  4. College of Artificial Intelligence, Nanjing Agricultural University, Nanjing, China, 210095
  5. School of Computer, Nanjing University of Information Science and Technology, Nanjing, 210044

• 期刊: IEEE Internet of Things Journal (中科院2023 一区)

文章内容

研究背景

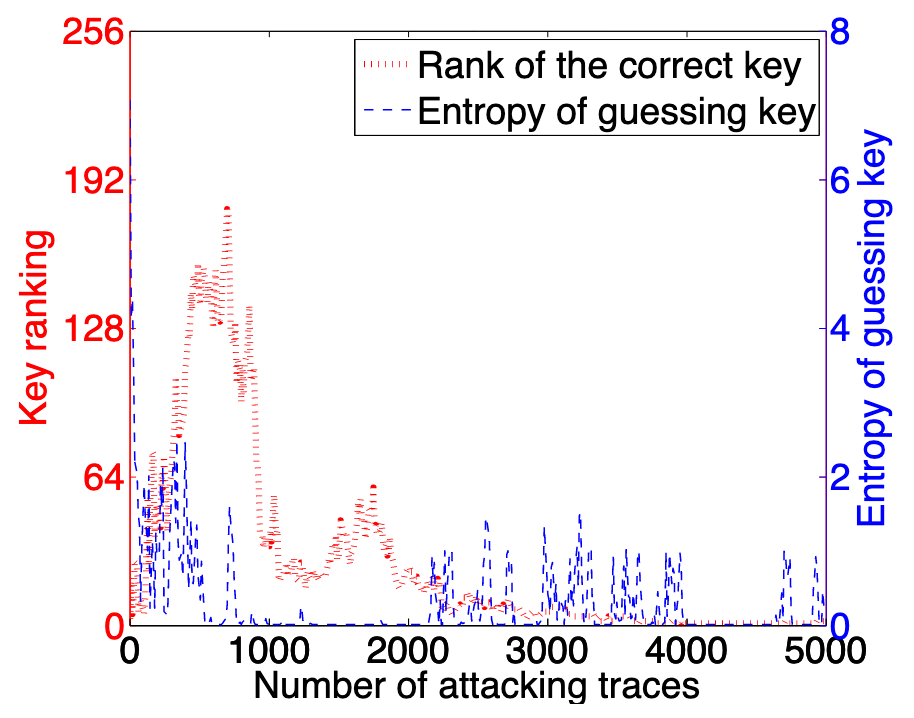
建模类侧信道攻击已经对硬件设备构成了严重的影响，然而在实际的攻击场景，单条能量迹往往无法成功恢复出密钥，攻击者需要根据多条能量迹来计算出密钥排名，通过累加的方法来完成正确密钥的猜测，图 1中展示了，在使用了 200,000 条能量迹进行建模的前提下，密钥恢复大约需要 4000 条攻击的能量迹。

已有工作存在的问题

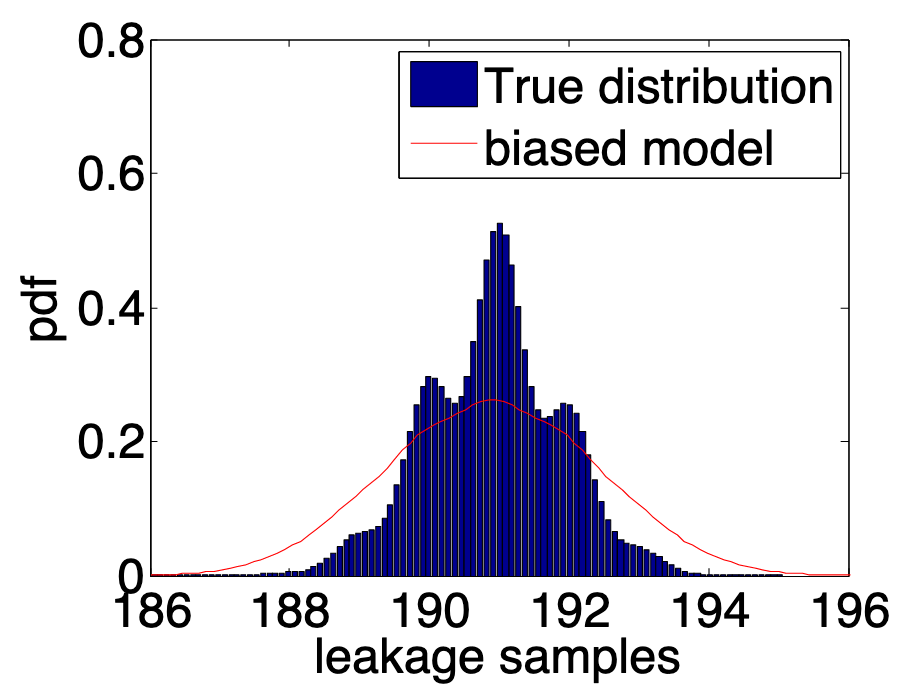
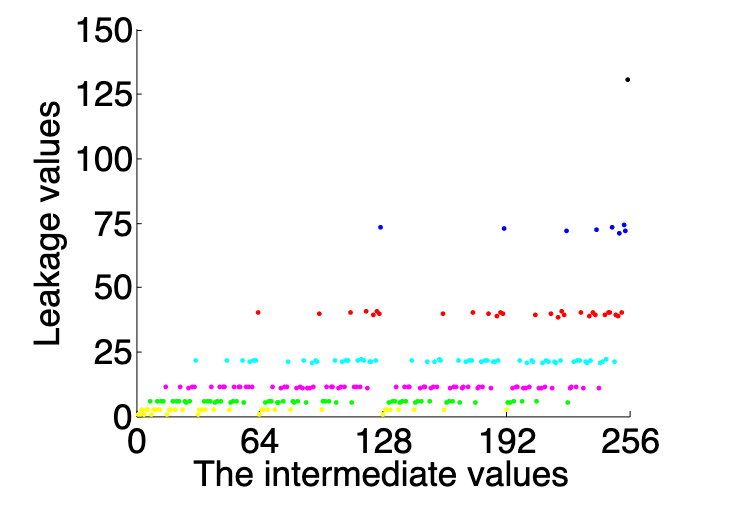
现有选择明文攻击大多基于 HW 和 ID 泄露模型，忽视了现实的情况：泄露往往是非线性的，如图 2 所示。此外，神经网络模型往往被视作一个黑盒，缺乏可解释性，分析者并不知道输入数据的变化是如何影响深度学习模型的输出的。

本文贡献

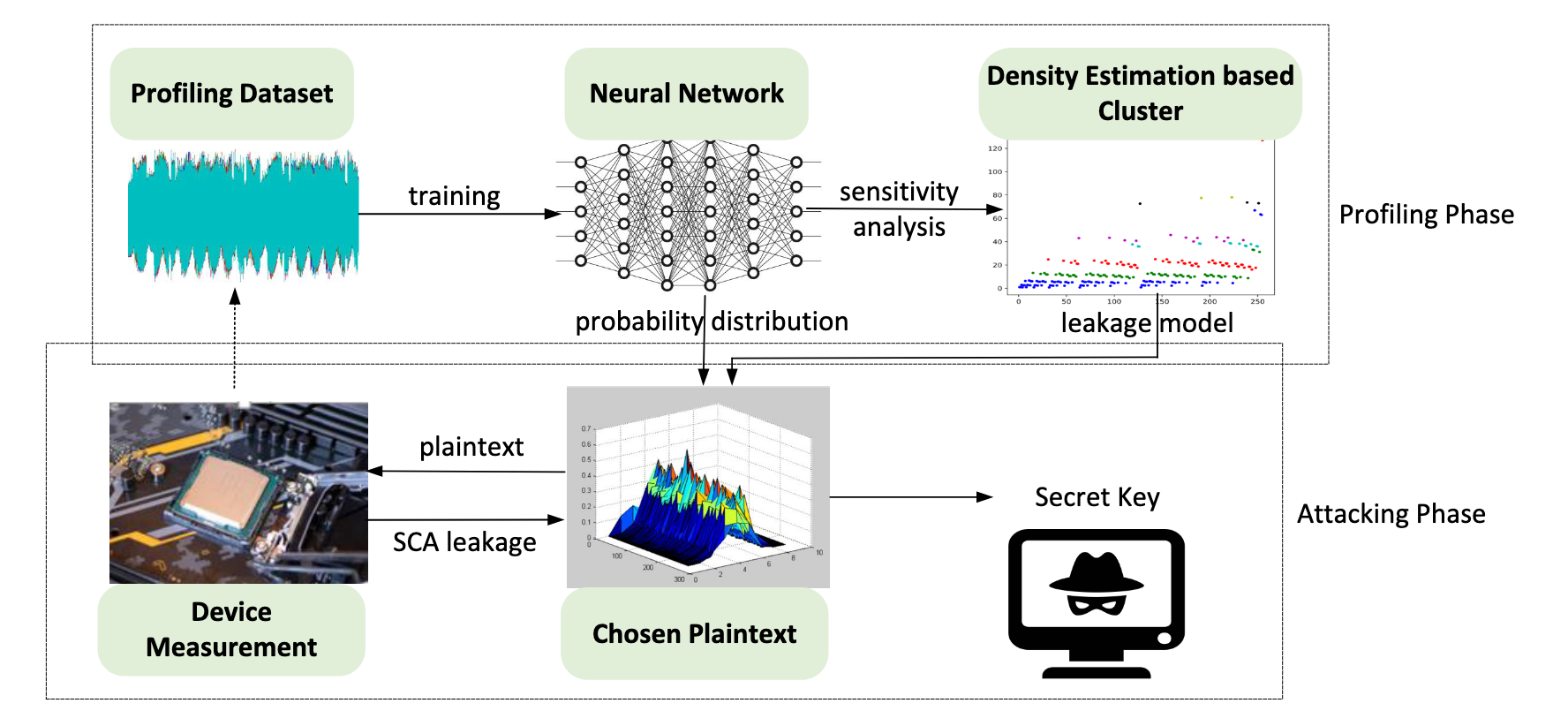
该论文提出了一种自适应选择明文的侧信道攻击方法，首次将选择明文的策略引入到深度学习侧信道攻击中。

1. 建模阶段：

实验步骤

敏感性分析（sensitivity Analysis）

$$ \begin{equation} T(Z) = \beta_{0} + \sum_{U \in \mathbb{U}_d} \beta_UZ^U + \varepsilon \end{equation} $$

其中，$Z$表示中间值的二进制形式，$\varepsilon$为噪声，集合$\mathbb{U}_d$=$ {U|U \in \mathbb{F}_2^{n}, HW(U) < d}$，这里，$Z^U=\prod_{j}^{n-1}z_j^{u_j}$，$z_j$表示二进制中间值$z$的第$j$位。

这里论文里的描述$u_j$ denotes the bits of $U \in F_2^n$\ $ {0}$ ，表示 U 是集合 F上的非零元素，举个例子 $u=00000001$，则 $u_0=1$(为什么要排除 0，当全部为 0 时，在二元域上，$z_j$不论是多少都会被计算为 1，那么公式1到最后就会直接变成 $T(z)=\beta_0 + \beta_0 + \varepsilon$

随后，对$Z^U$进行泰勒展开，可得：

$$ \hat{Z}^U \approx Z^U + \nabla f^T(l) \cdot \Delta l $$

这里，作者增加了一个很小的扰动$\delta$，使得$\nabla \hat{f}^T(l)=\nabla f^T(l) + \delta$，以此来判断哪些部分对模型的预测更重要，因为对于模型来讲，当对于$l$可以精确预测的时候，轻微的扰动是无法明显影响到模型的最终预测的置信度的。

基于自适应选择明文的深度学习侧信道分析框架

泄露模型

$$ \beta_U = 1 - \frac{E(|\hat{Z}_i^U - {Z}_i^U|)}{\max_{U}E(|\hat{Z}_i^U - {Z}_i^U|)} $$

聚类

基于上述灵敏度计算结果，将均值漂移用于分析的假设泄漏。均值偏移聚类不依赖于距离度量，因此不需要特征缩放预处理，使均值偏移更具灵活性和自适应性。图 x展示了均值漂移聚类之后的泄露模型，将不同中间值划分成不同的簇，以此来构成泄露模型，在图 6 中可以看到，一共分为了 7 个簇，也就是总共分为 7 类（和 HW 原理类似）。

Mean-shift聚类算法是一种基于密度的非参数聚类方法，其核心思想是对于每个样本点在特征空间中滑动一个窗口，计算其在窗口内所有点的加权平均位置来更新自身的位置，往局部密度最大的位置移动，直到达到某个停止条件，从而将其归类到相应的簇中。 – 知乎

$$ t_r^{r+1} = m(t_i^r) \\ m(t_i^r) = \frac{\sum_{t_j^r \in N(t_i^r)} K_D(t_j^r - t_i^r) t_j^r}{\sum_{t_j^r \in N(t_i^r)} K_D(t_j^r - t_i^r)} $$

这里，$N(t_i^r)$是$t_i^r$周围的能量迹区间，$K_D$是核密度函数，$m$是平均漂移向量。最后，泄露模型定义为$L(Z)={j|T(Z) \in C_j}$，经过计算得到泄露分布如图 x 所示。

选择明文攻击(重要)

$$ \hat{H}_{q_i}(K) = - \sum_{k^*}Pr(k^*) \log_2Pr_i(k^*) $$$$ \hat{H}_{q^*_{i+1}}(K) = \sum_{\hat{l}_{q_{i+1}}^K}Pr(\hat{l}_{q_{i+1}}^{K})\hat{H}_{q^*_{i+1}}(K|\hat{l}_{q^*_{i+1}}^K) $$

等式左边：对于第$i+1$个明文$q$，计算当前的密钥熵。

等式右边：

对于 CNN 模型，作者直接选择使用了 Zaid 那篇文章中针对 ASCAD 数据集的结构，如图 4 所示。

实验结果

泄露评估

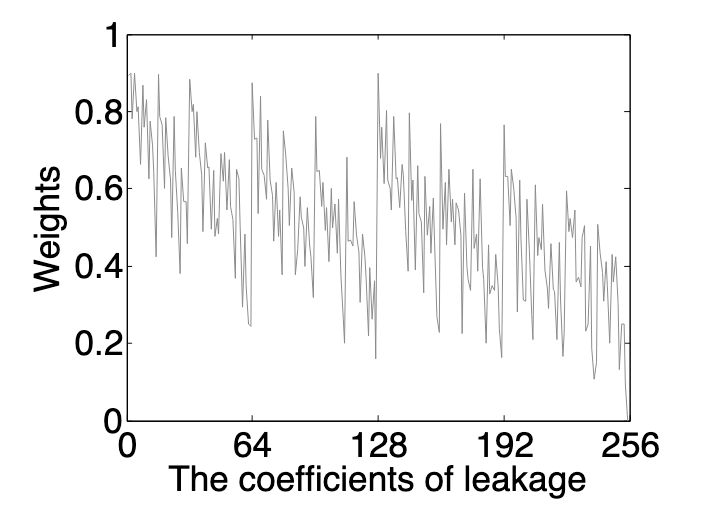
在泄露评估时，首先训练出一个神经网络模型，在第一层中加入扰动，这里作者设置的扰动因子大小为 1e-3,以此为基准，扰动后权重随着泄露系数（中间值）的增大逐渐降低，如图 5 所示。

随后，通过均值漂移（Mean-shift）聚类的方法，

选择明文攻击

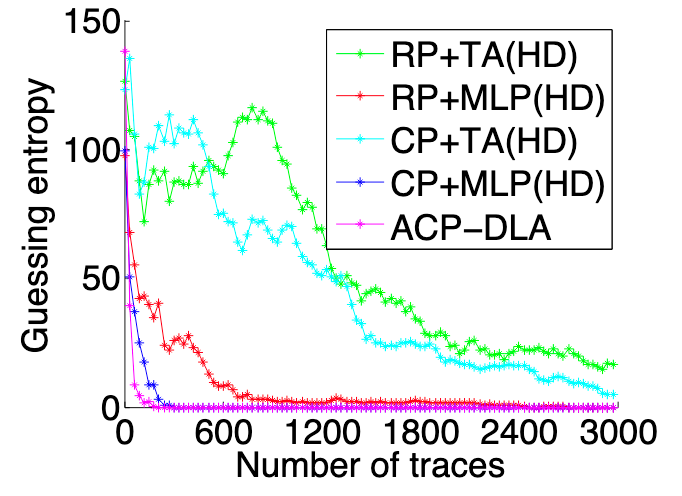
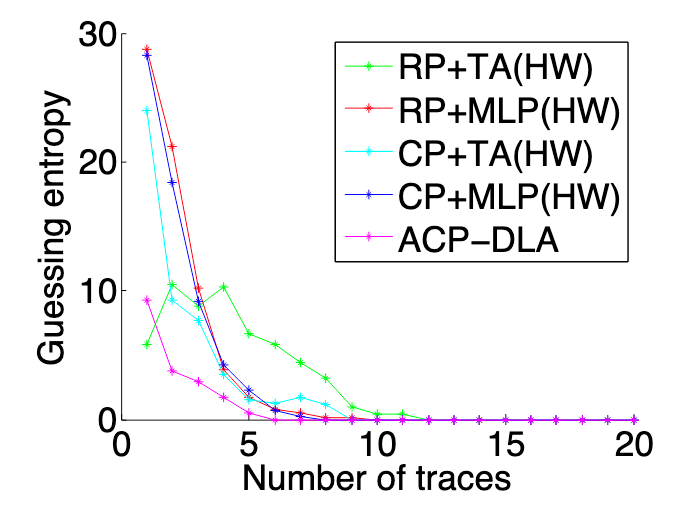
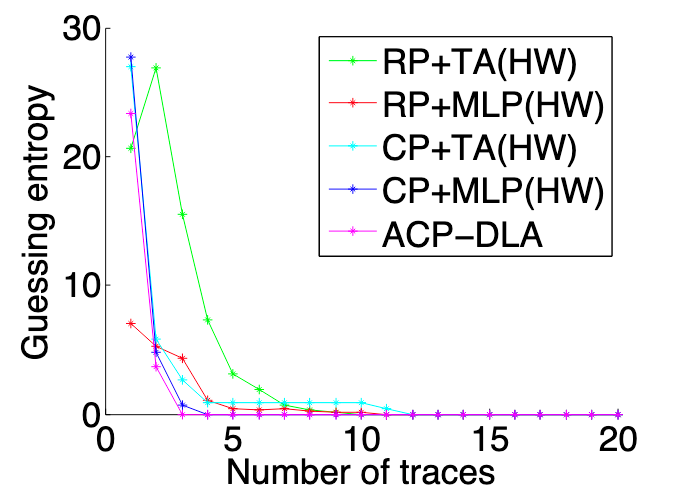
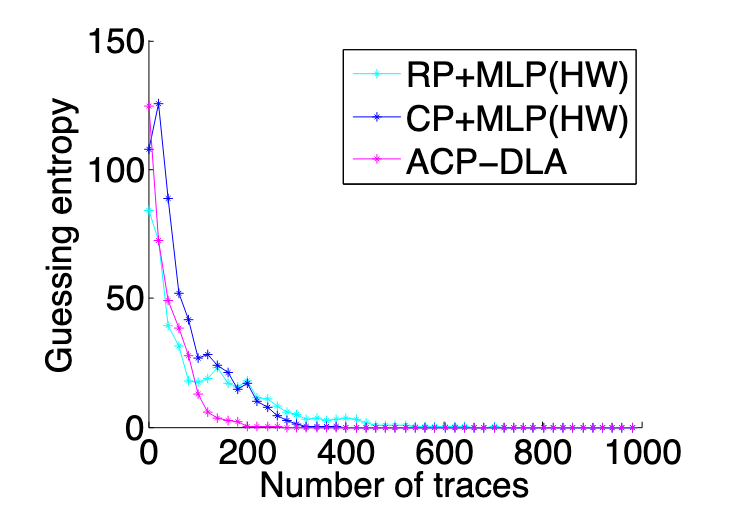
在攻击阶段，通过分析当前的能量迹，基于选择明文策略来选择指定的明文，以此明文进行加密生成能量迹，重复此步骤，直到猜测熵收敛到 0，在不同实现上攻击得到的猜测熵收敛曲线如图 7 、8、9和图 10 所示。可以看出本文提出的 ACP-DLA（基于自适应选择明文的侧信道攻击）的方法得到的结果要优于其他方案。

RP （Random Plaintext）指的是随机明文攻击，CP(指的是传统的选择明文攻击方法)，TA 是模板攻击，HD 是汉明距离。

总结